563. Простое уравнение
Петя нашёл в
книге простое математическое уравнение: a*x + b*y = 1.
Его интересуют
только целочисленные решения этого уравнения и только те, в которых x ≥ 0. Помогите Пете их найти.
Вход. В первой строке задано количество тестов
t (0 < t < 21). Каждая из следующих t
строк содержит два числа a и b (0 ≤ a, b ≤ 231).
Выход. Для
каждого теста выведите в отдельной строке одно решение уравнения: минимально
возможное неотрицательное значение x
и соответствующее для него целое значение y. В случае отсутствия
решения выведите “No
Solution”.
|
Пример входа |
Пример выхода |
|
3 77 51 10 44 34 79 |
2 -3 No
Solution 7 -3 |
РЕШЕНИЕ
расширенный
алгоритм Евклида
Анализ алгоритма
По заданным a и b
при помощи расширенного алгоритма Евклида находим такие d = НОД(a, b), x0
и y0, что a*x0 + b*y0 = d. Поскольку решается уравнение a*x + b*y = 1, то при d > 1 решения не существует.
Теорема. Все решения
диофантового уравнения a*x + b*y = 1 описываются множеством
 ,
,
где (x0,
y0) – частичное решение
исходного уравнения, k Î Z.
Подставим пару (x0 + kb, y0 – ka) в
уравнение a*x + b*y = 1:
a*(x0 + kb) + b*( y0 – ka) = 1,
ax0 + akb + by0 – bka = 1,
ax0 + by0 = 1, что верно
Для того чтобы x было минимально возможным
неотрицательным значением, необходимо чтобы k
было наименьшим, для которого x0
+ kb ≥ 0. Или ![]() . Наименьшим целым k,
которое удовлетворяет последнему неравенству, будет
. Наименьшим целым k,
которое удовлетворяет последнему неравенству, будет ![]() . Для этого значения k
следует найти и вывести решение.
. Для этого значения k
следует найти и вывести решение.
Поскольку
расширенный алгоритм Евклида находит такое решение (x0, y0),
для которого сумма |x0| +
|y0| минимальна, то при x0 < 0 искомое решение (с
наименьшим неотрицательным значением x)
равно
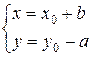
Если в частичном
решении (x0, y0) выполняется неравенство x0 ≥ 0, то оно само и
будет решением задачи.
Пример
Найдем частичное
решение уравнения 7x + 11y = 1 с минимально
возможным неотрицательным значением x. После запуска
расширенного алгоритма Евклида получим частичное решение x0 = -3, y0
= 2. Действительно,
7x0 + 11y0 = 7 * (-3) + 11 * 2 = 1
Тогда ![]() =
= ![]() = 1. Искомым решением уравнения
будет
= 1. Искомым решением уравнения
будет
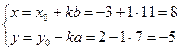
Проверка: 7 * 8 + 11 * (-5) = 56 –
55 = 1.
Реализация алгоритма
Функция gcdext реализует расширенный алгоритм Евклида.
По заданным a и b находятся такие d, x и y,
что a*x + b*y = 1.
void gcdext(long long a, long long b, long long &d,
long long &x, long long &y)
{
if (b == 0)
{
d = a; x = 1; y = 0;
return;
}
gcdext(b, a % b, d, x, y);
int s = y;
y = x - (a / b) * y;
x = s;
}
Основная часть
программы. Читаем входные данные.
scanf("%d",&tests);
while(tests--)
{
scanf("%lld
%lld",&a,&b);
gcdext(a,b,d,x0,y0);
Если НОД(a, b)
> 1, то решения не существует.
if (d > 1)
printf("No Solution\n"); else
{
Если в решении (x0, y0), найденном
расширенным алгоритмом Евклида, x0 < 0,
то пересчитаем его по указанной в анализе алгоритма формуле.
if (x0 <
0) x0 += b, y0 -= a;
printf("%lld
%lld\n",x0,y0);
}
}
Java реализация
import java.util.*;
public class Main
{
static long[] GcdExtended(long a, long b)
{
long res[] = new long[3]; // d, x, y
if (b == 0)
{
res[0] = a; res[1] = 1; res[2] = 0;
return res;
}
res = GcdExtended(b,a % b);
long s = res[2];
res[2] = res[1] - (a / b) * res[2];
res[1] = s;
return res;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int tests = con.nextInt();
while(tests-- >
0)
{
long a = con.nextLong(), b = con.nextLong();
long res[] = GcdExtended(a,b);
if (res[0] > 1)
System.out.println("No Solution");
else
{
if (res[1] < 0)
{
res[1] += b; res[2] -= a;
}
System.out.println(res[1] + " " + res[2]);
}
}
con.close();
}
}